ここで示す方法はかなりタフな方法であるが、直接的であり一般性を失わないので、方法的な意味での近似の評価を避けることが出来る。詳細は以下の論文に詳しい。
H. Witala et al., Few-Body Systems 3 (1988) 123
W. Gloeckle et al., Phys. Rep. 274 (1996) 107
問題は以下の方程式を解くことである。
（３.９９）
３体の部分波チャンネルを導入して表せば、
（３.１００）
となり、２章で示したように、t-マトリックスと粒子交換演算子は
（３.１０１）
（３.１０２）
で与えられる。ここで、
, 
は
（３.１０３）
（３.１０４）
このことから、（３.１００）式はもう少し具体的に書けて、
（３.１０５）
ここで、初項の t P は、
（３.１０６）
（３.１０７）
と与えられる。但し、α_dは２核子の束縛状態（重陽子）のチャンネル 
に関連したものだけを取り出す。この初項の計算は特異点がないために簡単である。一方、積分核の方は、グリーン関数から生じる特異点と
t
マトリックスの持つ重陽子の特異点の２つがある。重陽子の特異点（
）は２体問題でのものと同じ性質のものであるいから、ここでは省く。（３.１０５）式を見ると、x
と q" の積分が必要である。 xについての積分を示すと、グリーン関数とその他の部分（f(x)）を
（３.１０８）
但し、
（３.１０９）
と取り出す。q と q"
によって、
となる場合があり、積分は
（３.１１０）
のように計算されなくてはならない。ここで、第２項は問題なく数値積分が可能で、第１項は解析的に求める。
（３.１１１）
未だ、特異点が消え去らず、q-q" の面で見れば、２つの線上で対数発散が生じる。
（図）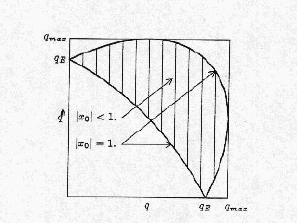
月の形の内部では虚数部分が（３.１１１）式の２項から生じることになる。残される問題はこの対数発散を上手に扱うことであるが、１位の特異点と異り、積分点をその２つの線の近くまで十分とれていれば精度を得ることができる。任意の点の値を準備する必要がでてくるが、それは内挿の精度にかかってくる。
積分方程式は、ガウス積分点等を用いることで、離散的な行列方程式になる。そのマトリックスのランクは６万以上になる。即ち、最終的には、６万個の未知数の１次連立方程式を解くことになる。現代のスーパーコンピュウターをしてもこの高次元方程式を直接解く事は不可能である。我々はPade
近似法という方法を用いて、多重散乱の級数を繰り返し生成し、解を求めている。これ以上はかなり技術的な問題になるので、立入らない。
現実的ポテンシャルを使い、精度は１％以下に抑えることで、十分実験データに耐えられる計算を行うことができている。陽子の入射エネルギーが
１５０ MeV 以上になると、（３.９９）式の部分波展開での計算が困難になり、部分波展開を行わない方法が必要になるであろう。