３核子系における測定量は大変豊富である。偏極を考えなければ、弾性散乱と３核子分解（ブレイクアップ）に分類できる。弾性散乱の場合、前に示した組み替え
演算子 U を使って、散乱振幅は
（３.８８）
によって与えられ、この絶対値の２乗は微分断面積を与える。
（３.８９）
勿論、この時、始状態のスピンについて平均をとり、終状態のスピンについては和をとる。
ブレイクアップの場合はもう少し複雑で、
（３.９０）
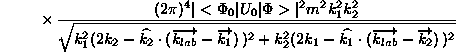
のように微分断面積は求まる。ここで、
, 
は実験室系での運動量で、
は入射粒子の運動量。ここで、新しい変数 Sを導入した。
S
は運動学的に描かれる弧の長さを意味する。それを詳しく説明する。実験室系で、エネルギーと運動量の保存則は
（３.９１）
（３.９２）
と書けて、
を消去すれば、（ 
）
（３.９３）
（３.９４）
を得る。（３.９４）式は k1 と
k2の座標面で楕円を描く。入射粒子の
と ,
の向きによって様々な楕円を描くことになる。以下の図では、E1-E2の面と共に物理的に許される領域を表している。エネルギーは常に正であることから、図で、黒丸で表した領域だけが物理的な事象を起し得る所となる。
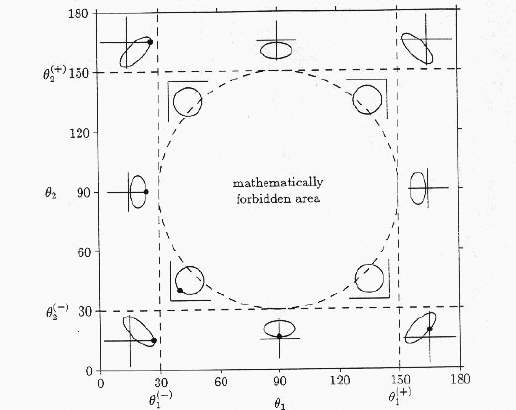
正確に変数 S を定義すれば、
（３.９５）
で、E1-E2面での円弧の長さに対応する。S＝０の出発点を黒丸で示した所とし、時計周りでその長さを測る。
次に、偏極量について簡単に説明する。これについての詳しい定義は、Gerald
G. Ohlsen 等によってなされ、学祭的な合意を得ている。（G.G.
Ohksen, Rep. Prog. Phys. 35 (1972) 717-801.）
例えば、核子の 偏極分解能 
（良く、重陽子のものと間違えられる）は、
（３.９６）
で与えられ、重陽子の テンソル分解能 
は
（３.９７）
ここで、
は
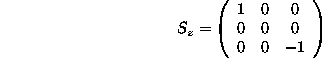
である。
また、核子から核子への スピン偏極移行量Kyy'
は、
（３.９８）
で求まる。これらの偏極量は弾性散乱とブレイクアップの両方にあり、散乱振幅を入れ替えるだけで、同様に計算される。