散乱を扱う場合、波動関数よりもむしろ遷移振幅を扱う方が多く、その方が断面積を計算するのに便利である。散乱振幅
Uij
に対する方程式を導こう。これは三つ巴の方程式から、直接導かれる。（３。１４）式から、
（３.２７）
と定義できて、（３.２５）式と（３.２６）式を使えば、右辺は
（３.２８）
となる。定義（３.１７）式と（３.２０）式を用いれば、
（３.２９）
（３.３０）
更に、
（３.３１）
を得る。また、（３.２９）式と（３.３０）式から始れば、（３.２４）式を用いて、
（３.３２）
（３.３３）
も求めることができる。これらは結合した方程式で、もっと簡単に書き表せば、
（３.３４）
となる。ここで、
、また 
の意味である。これを AGS
方程式と呼ぶ。
Alt et al., Nucl. Phys. B2 (1967) 167.
実際には、３核子は同一粒子として扱うので、反対称化した状態を用いる。
（３.３５）
従って、
は粒子２と３に対して反対称であり、
は１と３に対し、
は１と２に対して反対称状態が仮定される。更に、粒子交換演算子
P
を使えば、明かに
（３.３６）
（３.３７）
の関係を得る。従って物理的状態の
は
P
を使って、
（３.３８）
と書表せる。この事は、（２.２１）式で示した事と同じである。例として、終状態がチャンネル１になる散乱振幅 U1 を考えよう。定義から、
（３.３９）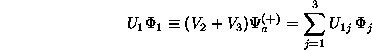
となり、チャンネル２と３に対する振幅（U2, U3）も同様に求まる。
（３.４０）
ここで、AGS 方程式（３.３４）をそれぞれのチャンネルに対して、明らさまに書き直せば、
（３.４１）
となるから、Ui との関係（３.４０）を使えば、
（３.４２）
（３.４３）
となる。ここで、もう一度 粒子交換演算子 P を使えば、
（３.４４）
（３.４５）
とできるので、あえて Ui に添字を付ける必要がなくなる。
（３.４６）
よって、（３.４３）式は簡単になり、１つの式で書ける。
（３.４７）
この方程式は初期の段階では、２体の散乱マトリクス t を分離型にしたり、
（３.４８）
色々な技術を用いて解かれてきた。この場合、U は弾性散乱の振幅として次の様に書き表せる。
（３.４９）
次に、３つの粒子がバラバラに分解する場合を考えよう。漸近的な状態 
は、自由なチャンネルだから、
（３.５０）
となり、明かに
（３.５１）
（３.５２）
に従う。また、散乱振幅 U0は
（３.５３）
で定義できるから、演算子 U0は
（３.５４）
と書けて、（３.２４）式から（３.２６）式の三つ巴を用いて、
（３.５５）
（３.５６）
（３.５７）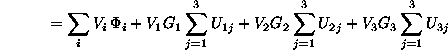
（３.５８）
（３.５９）
（３.６０）
最後の式で、又添字を省いた。ここで、U0は３粒子が分解するので、（３.６０）の第１項のオエネルギー殻上に乗らない。従って、それからの寄与は全くなく、
（３.６１）
となる。
（３.６２）
のSchroedinger方程式から（３。５３）式の定義は正しいことがを調べてみよう。
このブレイクアップのチャンネルに対しても、非斉次の項は考えられないことから、
（３.６３）
（３.６４）
と書ける。ここで、座標空間での３体自由グリーン関数は知られていて,
（L.S. Rodberg, R.M. Thaler, Introduction to the Quantum
Theory of Scattering, page 123)
（３.６５）
H2 はハンケル関数で、X
は
（３.６６）
により与えられる。漸近状態を調べるために、
と 
を∞にもって行けば、
（３.６７）
で、更に、極座標を導入して
（３.６８）
（３.６９）
これより、
（３.７０）
と
（３.７１）
（３.７２）
（３.７３）
を使い、更に
（３.７４）
から、結局、
（３.７５）
となる。ここで、p , q は
（３.７６）
（３.７７）
である。x, y を∞にもって行けば、明かに p ,q のヤコビ運動量と角度αによって決まる。また（３.７５）式を（３.６４）式に代入すれば、ブレイクアップの漸近的な形が分る。
（３.７８）
このことから、ブレイクアップの遷移振幅を読み取れる。
（３.７９）
完全に反対称的な状態は斉次な
LSE
方程式を満し、それ故、（３.５４）式はブレイクアップの振幅であることが確認できる。
さて、これらの２つの過程の振幅 （ U and U0 ）を同一粒子の場合、まとめて書くと、
（３.８０）
（３.８１）
で、求められる。ここで、U を解く代りに次の量を定義すれば、
（３.８２）
（３.８０）式は
（３.８３）
によって、解くことになり、この T を使えば、U とU0は、
（３.８４）
（３.８５）
で与えられる。
ここで、T は闇雲に導入した訳でなく、３体の
t
マトリックスとしての役割りを演じることを示そう。演算子
T
は定義から、
のチャンネルに働くので、明らさまに書けば、
（３.８６）
これを、繰り返し代入していけば、
（３.８７）
これは、グラフで書けば、
（グラフ）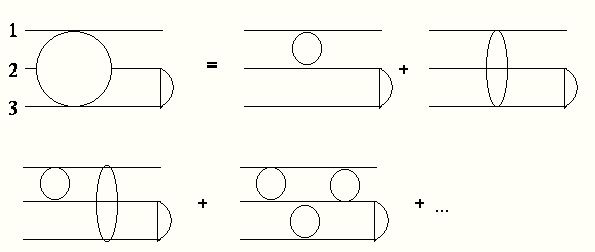
のようにより見透しの良い物理的な、メカニズムを説明する。ここで、積分核（t P G0 ）において、 演算子 P により必ず異なるペアで t マトリックス結合することが、方程式を解けるものにしていることを数学的に示すことができる。（ここでは、深入りしない。）