k1とk2を独立な核子の運動量とした場合、相対的な運動量は、
(1.1)
と与えられ、運動量の固有状態は、
(1.2)
で書き表す。これは、
(1.3)
により規格化することができ、その固有状態は
(1.4)
どのように核子-核子散乱を記述するか?
k1とk2を独立な核子の運動量とした場合、相対的な運動量は、
(1.1)![]()
と与えられ、運動量の固有状態は、
(1.2)![]()
で書き表す。これは、
(1.3)![]()
により規格化することができ、その固有状態は
(1.4)![]()
の相対運動の自由ハミルトニアンより与えられる。 mは核子の質量である。ここで、Vを核子間のポテンシャルとすれば、散乱のシュレディンガー方程式は次のように与えられ、
(1.5)![]()
それは、積分方程式即ち、リップマン-シュウィンガー(Lippmann-Schwinger)方程式LSE を導く。
(1.6)![]()
(1.7)![]()
先ず、座標空間表示で考えることにしよう。 運動量 p に対応する共役な座標は
(1.8)![]()
であるから、これも同様に規格化ができ、
(1.9)![]()
となる。この規格化によって、
(1.10)![]()
という平面波を関数化できる。さて、このことを使って座標空間での自由グリーン関数
G0を導いてみよう。
(1.11)![]()
(1.12)![]()
(1.13)![]()
(1.14)![]()
![]()
(1.15)
これを、通常の方法で計算すれば、
(1.16)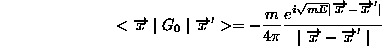
を得る。これは、x’から xの 出ていく波動を表し、これを使えば、座標表示での LSE は次のように書ける。
(1.17)![]()
(1.18)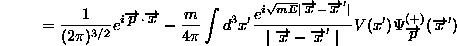
さて、ここで局所的ポテンシャルを仮定し、
(1.19)![]()
漸近的な振舞いとして | x | が無限大の極限での散乱波は次のように書ける。
(1.20)![]()
f(x^)は xの方向にだけ依存する関数で、散乱振幅と呼ぶ。これを局所的ポテンシャル
V
を使い、具体的に表せば、
(1.21)![]()
となり、このことから散乱後の運動量は p’と解釈できる。
(1.22)![]()
ここで、遷移振幅 t を導入しよう。
(1.23)![]()
(1.24)![]()
この t を用いれば、全ての散乱のオブザーバブル(測定量)を得ることができる。実は、この遷移振幅 t は積分方程式から直接求まる。(1.24)式を使って
(1.25)![]()
と書けることに気付けば、(1.7)式は
(1.26)![]()
(1.27)![]()
と式変形されて、 | p > を更に省くことをすれば、
(1.28)![]()
を得る。この表記を LSE のオペレーター表示という。
ここで、t の簡単な物理的な解釈を考えてみよう。
(1.29)![]()
(1.30)![]()
これは、V の相互作用によるボルン級数と呼ばれるもので、Vの羃の順に和を取ったものである。それぞれの項は V と G0 が交互に現れ、粒子数を増やしてもこの構造は一般的である。それを、もっと視覚化すれば、多重散乱のイメージが理解できる。
(図 1.1)
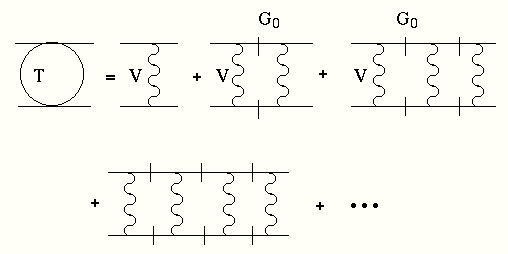
ここで、波線は V による相互作用を表し、横に水平に引いた2つの線は自由グリーン関数G0を表している。明らかに、(1.30)式から
(1.31)![]()
この様に逆に t を定義して、(1.28)の LSE を導く。
(1.32)![]()
(1.33)![]()
これらの多重散乱の級数展開の方法はより一般的で、相対論的な2体の散乱方程式である
Bethe-Salpeter 方程式の場合にも通じる。但し、G0
が我々の扱っているものと異なる。