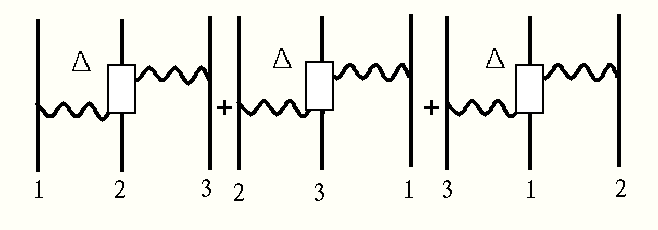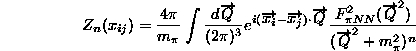• ２.５ ３体力の効果

３体力についての論文は豊富にあり、そのいくつかを揚げる。
M.R. Robilotta, Few-Body Systems Suppl. 2 (1987) 35
B.H.J. McKeller, Lecture Notes in Physics 260 (1986) 7
S.A. Coon, Few-Body Systems, Suppl. 1 (1986) 92
P.U. Sauer et al, Europhysics News 15 (1984) 5
R.B. Wiringa, Phys. Rev. C43 (1991) 1585
D. Pluemper et al,Phys. Rev. C49 (1994) 2370
最近のカイラル摂動理論によるものとしては、
U. van Klock, Phys. Rev. C49 (1994) 2932
等である。ここでは、それぞれの３体力についての議論は行なわない。勿論、これらは核力（２体力）に関した問題であり、物理はそこにある。しかしながら、ここでは技術的な問題や、いかに Faddeev 方程式に組込むかについての議論に注目する。３体力のひとつのあり方として考えられるメカニズムは、２π中間子交換である。

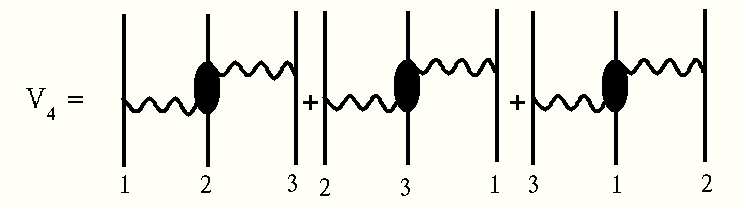
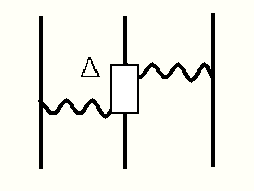
図に示した黒丸の部分は、π-N 散乱の散乱振幅(a)から、単純に核子が伝播する部分(b)を差し引いたものと解釈できる。

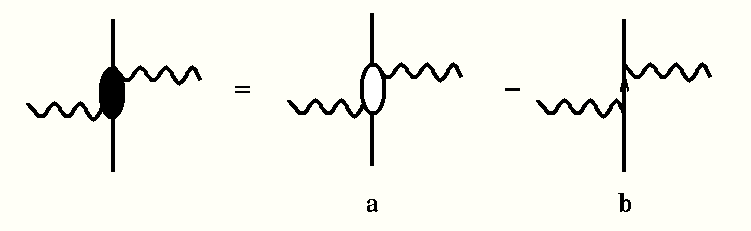
なぜならば、この伝播する項(b)を取り込んだ３核子の過程を考えれば、図のように

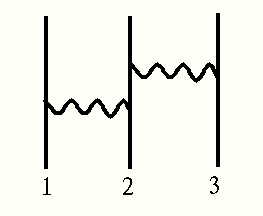
既に２体力で考慮したものに成ってしまい、同じものを二重に取り込むことになるからである。（V₁₂G₀V₂₃）
従って、（b）の項をπ-Nの振幅から取り除いたものを V₄としなくてはならない。一方、

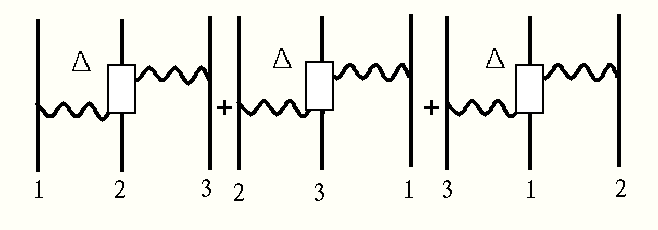
この場合、中間の核子に代る粒子が物理的な考えから必要で、具体的にはΔ粒子がある。明らさまに、Δ粒子を用いて３体力が提案されたものを Fijita-Miyazawa 力 （藤田-宮沢）と呼ばれている。
J. Fujita et al, Prog. Theor. Phys. 17 (1957) 360
低エネルギーでのカレント代数を考慮すると、Fijita-Miyazawa 力 の他に幾つか付加された項も含めた３体力の模型があり、代表的なものは、Tuscon-Melbouron 力 と呼ばれている。π-π交換について、その表式を書けば、

（２.８０）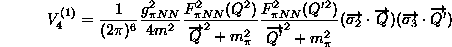

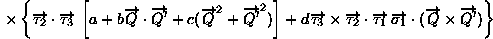
の様に与えられる。上につけた添字（１）は、図で示した３つの過程のなかで、真中の核子番号が１番になる項を意味し、他の項は循環あるいは反循環の粒子交換演算子によって求まる。

（２.８１）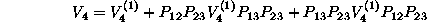

ここで、F＿πNN（Q）は強い相互作用の形状因子、また、Q やQ’はπの運動量を意味する。a,b,c,d の定数は理論的に与えられたり、実験的に決められなくてはならない自由度が残っている。この３体力は簡単に座標表示にも書き換えることができる。

（２.８２）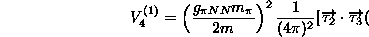

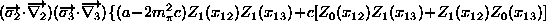
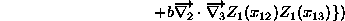
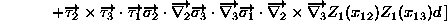
ここで、Z は次式で与えられる。

（２.８３）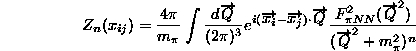

例えば、スピンやアイソスピンを無視して、更に a-項だけに注目すれば、これは、明かに２つのYukawa型の相互作用の積に成っている。しかしながら、見ての通り３体力はもう少し複雑である。
更に、π-πのみでなく、π-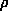 や 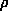- 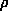の交換の効果を取り込んだ３体力もある。その場合、 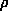 のスピンが１であるために複雑な形のスピン依存型の３体力になる。
 

次に、これらの３体力をFaddeev方程式に取り込むことを考えよう。先ず、Schroedinger 方程式から始める。

（２.８４）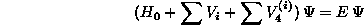

ここで、既に３体力は３つの部分から成ることを仮定している。しかし、この仮定は物理的には３核子の同一性となんら矛盾することではない。従って、２体力 V_ij の和と３体力の和はまとめることができて、Faddeev 要素は次のように定義できる。
（２.８５）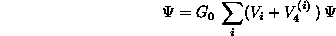
（２.８６）
（２.８７）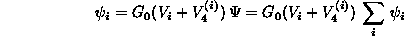
（２.８８）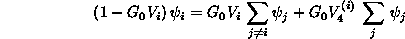
（２.８９）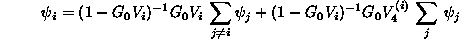
ここで、LSE の２体散乱行列 t は

（２.９０）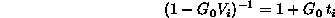

を満すことから、Faddeev 方程式は
（２.９１）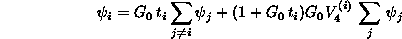
の様に書ける。更に、粒子交換演算子を使って書けば、見透しの良い形として、

（２.９２）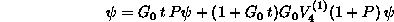

を得る。実際の計算では、これらを更に部分波に分解した形で解く必要がある。それについての詳細は、例えば、
W. Gloeckle, Lecture Notes in Physcs 273 (1987) 3
S. Coon et al, Phys. Rev. C23 (1981) 1790
を参照されたい。
３体力に用いている粒子交換演算子は（２.５７）式を使う方が便利である。また、部分波の扱い方は
D. Hueber et al, Few-Body System 16 (1994) 165
に詳しい。
（２.９２）式は解かれてる。
A. Stadlar et al, Phys. Rev. C44 (1991) 2319
この論文からいくつか結果を引用する。

残念ながら、現状ではπNNの形状因子に対する強い依存性があり、通常それは

（２.９３）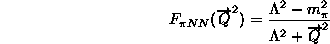

の形で与えられ、切断パラメーターΛに依って結合エネルギーが簡単に変ってしまう。
πー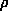 及び 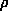-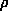の交換を考慮した計算が
A. Stadler et al, Phys. Rev. C51 (1995) 2896
にある。表には、適切な切断パラメーターを選んでの結果を示した。２体力で知られている切断パラメーターと比べて３体力は大きな値が必要であるが、表を見て分るように３体力によって実験値再現の希望が持てそうである。しかしながら、一方、OBEPQの場合を見るとかなり過結合になっていることから、２体力と３体力の整合性について更に研究する余地がある。

その方向での理論的な進め方のひとつは、トリトン内部のΔ粒子の励起を１つだけに留まらせず、２つ３つと増すことである。

（２.９４）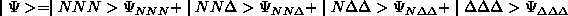

当然、これらの基底をSchroedinger 方程式に代入すれば、４つの連立した方程式を解くことになる。最近のこの方向での研究は
A. Picklsimer et al, Phys. Rev. C46 (1992) 1178
等にあり、先駆的な仕事は、Hajduk 等
Ch. Hajduk et al, Nucl. Phys. A405 (1983) 581; Nucl. Phys. A405 (1983)  605
よってなされた。そこでは、Δ粒子による引力的な部分は他の効果から生じる斥力的な部分と打ち消し合い、結局は２体力に近付き、また、ΔΔΔ の状態は非常に小さいが、NΔΔは無視できないというものであった。

２体力と３体力の整合性の叶った計算は、まだなされていない。

はじめにもどる