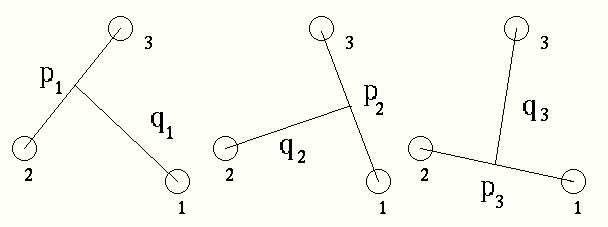
議論を簡単化するために、スピンとアイソスピンの自由度を無視する。同一粒子の場合、質量も同じと仮定することによって、ヤコビ座標を次のように導入できる。

(2.26)![]()
(2.27)![]()
これは、ペアを1=(23)に選んだ場合で、2=(31)、3=(12)に対しても、同様に、
(2.28)![]()
(2.29)![]()
(2.30)![]()
(2.31)![]()
ここで、後に大切になる関係を示しておく。
(2.32)![]()
(2.33)![]()
(2.34)![]()
(2.35)![]()
pi は(jk)のペア間の相対運動量で、qi は(jk)ペアの重心と第3粒子間の相対運動量である。
次に、3体の状態ヴェクトルを導入する。
(2.36)![]()
これは第一章で扱った様に、次式のように規格化できる。
(2.37)![]()
どのヤコビ座標系で表したかを明記することは、便利な場合がある。それを括弧の下に付けた。
(2.38)![]()
この表記は便利で、例えば
(2.39)![]()
は
(2.40)![]()
と書ける。
ファディーフ方程式を運動量表示で書こう。
(2.41)![]()
即ち、
(2.42)![]()
(2.43)![]()
で与えられ、G_0=1/(E-H0) の運動エネルギーH_0の部分は、それぞれのヤコビ座標を使って、
(2.44)![]()
(2.45)![]()
と書ける。更に、この H0の固有状態が(2.36)の状態と言うこともできる。G0は従って、基底に対して対角的であるから、
(2.46)![]()
ここて、t 演算子はポテンシャル V から求まり、2体系の p の変数にのみ作用する。
(2.47)![]()
q は第3粒子の運動量である。それが相互作用に関わっていないことから、その粒子を傍観粒子(spectator)と呼ぶことがある。 LSEをもう一度、3体の基底で見直してみれば、
(2.48)![]()
(2.49)![]()
![]()
(2.50)![]()
![]()
となり、(2.47)のポテンシャルと同じく、q に対するデルタ関数を添えることで求められる。
(2.51)![]()
ここで、t^ は2核子系でのt-matrix
で、そのエネルギー
E_2 = E - 3/4m q^2 で置き換わる。 ここで、エネルギーは
p
及び、p’に独立な変数であることに注意する。あくまで、エネルギー殻上(on-energy-shell)とは
p=p’=(mE)^1/2
の条件の意味で、非エネルギー殻(off-energy-shell)の
t-matrix
が必要になる。t^の
LSE
は、
(2.52)![]()
![]()
である。q が増加しても、2体系のエネルギーが減るわけだから、
E<0
の束縛状態の問題を扱うときは、常にグリーン関数
G_0
には特異点がない。従って、(2.43)のファディーフ方程式は、
(2.53)![]()
![]()
となる。ここで、技術的に最も面倒な扱いをしなくてはならない演算子は 粒子交換演算子で、これは、2つのデルタ関数に分解される。
(2.54)![]()
(2.55)![]()
(2.56)![]()
![]()
(2.57)![]()
![]()
このデルタ関数は(2.53)式の3つの積分の中、2つを消去する。(2.57)式をもう少し整理して、
(2.58)![]()
![]()
![]()
(2.58)式から、(2.53)式は
(2.59)![]()
![]()
![]()
と与えられる。このままでは、t-matrix とファディーフ要素 との間の積分は、p と q の6変数(2×3次元)を扱わなくてはならなくなる。これは、明かにトリヴィアルな仕事ではない。実際にそれを直接扱う方向もあるが、核力が主に S波や又はテンソル力による D 波によって、殆んど記述できることを期待すれば、部分波展開の方法により、変数を減らすことがでる。