•  １.６   重陽子の性質

LSE 斉次方程式（１.３８）式を（１.７０）式の基底で書き表すと、波動関数Ψ（ｐ）は

（１.９８）

となり、l ＝０または２、s＝j＝１、t ＝０を仮定すれば、次の連立積分方程式を得る。この量子数に対して重陽子は存在している。

（１.９９）

この方程式は数値的に解くことができる。現実的な核力は様々な測定量を再現するように作られる。この場合、測定量とは具体的に、

結合エネルギーEb=-2.2246 MeV
四重極子モーメント Q=0.2859 fm²
（但し、中間子交換流による理論的不確実さを伴う）
漸近的規格化定数 As = 0.8883 fm^-1/2
規格化定数の S 波、D 波の比  Ad/As  = 0.02564
 

重陽子の D 波の存在比 P_dは直接測定できない量で、これが原子核の結合エネルギーに大きく関係している。このことについては、後で詳しくのべる。一般に、小さな P_d 程、三重水素（トリトン）やヘリウム４（アルファ粒子）の結合エネルギーは大きくなる。

（１.１００）

さて、重陽子の中の１核子の運動量分布を考えてみよう。

（１.１０１）
（１.１０２）

ここで、
（１.１０３）

だから、
（１.１０４）

となる。ここで、
（１.１０５）
（１.１０６）

を使えば、
（１.１０７）

を得る。クレブッシュ - ゴルダン係数の性質
（１.１０８）

より、（但し、
  ）

（１.１０９）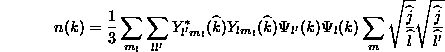

（１.１１０）
（１.１１１）

様々な現実的ポテンシャルによる１核子の運動量分布を次に示す。それぞれの核力の違いは 運動量kが １fm ^-1 を超えた辺りから見えはじめる。

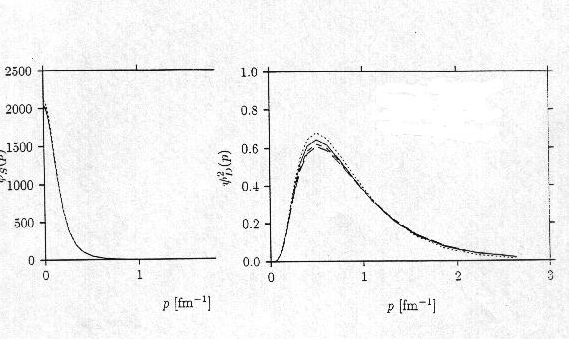
S 波                                                                                 D  波

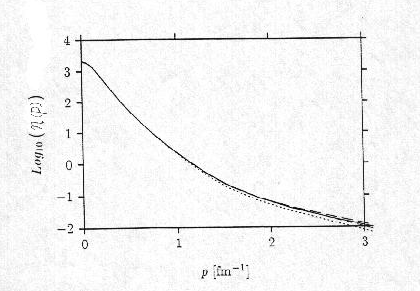
全波 = S 波  + D  波

_______________    RhurPot potential
_  _  _  _  _  _  _  _      AV18 potential
-----------      Nijmegen I potential
..................................     Bonn B potential
 
 

核子 - 核子の相関関数を考えてみよう。即ち、２つの核子が r の距離に存在する確率を関数化したもので、
（１..１１２）
（１.１１３）
（１.１１４）

と定義できる。この場合、座標空間での波動関数は運動量表示の波動関数のフーリエ変換によって得られる。

（１.１１５）
核子ー核子の相関関数をS 波と D 波に分けてグラフにした。近距離では相関が小さくなっているのは、核力の近距離で強い斥力が働いていることの現れである。

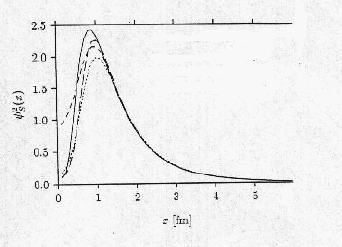
S 波

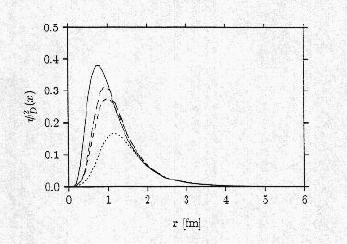
D  波

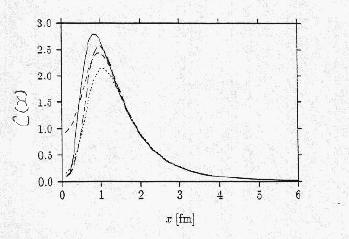
全波 = S 波  + D  波
 

_______________    RhurPot potential
_  _  _  _  _  _  _  _      AV18 potential
-----------      Nijmegen I potential
..................................     Bonn B potential
 

•  １.７ 現実的核力