色々な現実的なポテンシャルを用いて、トリトンの結合エネルギーが計算されている。以下に示した表では、jmax
をどこまで取り込んだかによって、それぞれのポテンシャルに対する結合エネルギーを示した。
(表) 
実験値 8.48MeV に比較する精度としては、jmax=4 で十分であることが分る。この表で示したポテンシャルは、第一章で述べた CIB(荷電独立性の破れ)を考慮した計算もあり、それは中性子-陽子ポテンシャルと中性子-中性子ポテンシャルを区別する。それらを考慮した計算の有効的な扱いとして、特に1S0状態に対して、
(2.79) ![]()
の混合を行えば、アイソスピンt=3/2に対するチャンネルを新しく開かなくても3体計算は十分精度の良い計算ができることが知られている。
(H. Witala et al, Phys. Rev. C43 (1991) 1619)
T =3/2の混合はCSB(荷電対称性の破れ)から生じるが、非常に小さな寄与であることが示されている。(2.79)式を使ったCIBの計算を表にする。
(表) 
この中で局所的なポテンシャルはNijm II, Nijm 93, AV18で、ほとんど同じ結合エネルギーを与えている。Nijm
Iポテンシャルはそれらに対して弱い非局所性があり、そのために
100keV の違いがある。更に、完全に非局所的ポテンシャルである cd
Bonn は、約350keVの差がある。なぜ非局所的ポテンシャルが3体系では引力的に働くかの明確な理由は、まだ説明されていない。
実験値と比較すれば、500から800keVの違いがある。結合エネルギーの大きさと比較すれば、この違いが大きい
ように見える。しかし、結合エネルギーは正の運動エネルギー(45MeV-55MeV)と負のポテンシャルエネルギー
の相殺から得られることを考えると、そのくいちがいはポテンシャルエネルギーに対して、1%程度のものと言うこと
もできる。このことについて、3体力の所でもう一度ふれることにしよう。
さて、運動量分布関数 n(k)や相関関数 C(r)を重陽子の場合と同様に求めることができる。この場合、重陽子と比べるとトリトンはより高い密度である事がわかる。
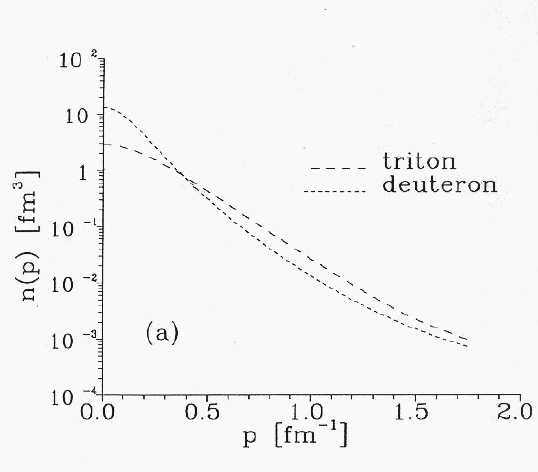
それは、C(r)のグラフを見れば明かである。ここで、C(r)は通常の規格化による。1fm 辺りでトリトンが大きな相関密度をもっているのは、トリトンの方が重陽子よりも多くの結合エネルギー( 7.48MeV > 2.23MeV)をもっていて、そのために相関関数はトリトンの方が早く0に近付くためである。また、原点では相関が少くなる理由は、核力の近距離での強い斥力によるものである。このことは、第3番目の核子に関係なく同じ振舞いをする。
一見、同じような振舞いをする関数に見えるが、どのような核力の成分に依ってできているかを調べることは興味深
い。2核子間の部分波によって調べてみれば、明かになる。
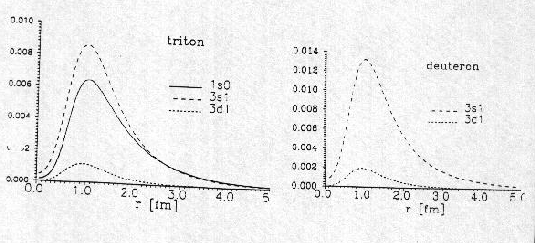
(グラフ)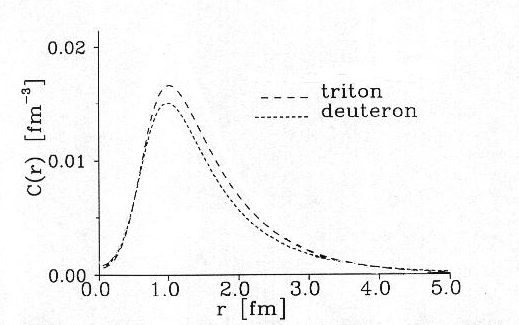
周知のように、重陽子は3S1-3D1から成る。トリトンは、2つだけではなく多くの成分より成る。グラフに示したように、トリトンには1S0の成分が3S1の状態と同程度に含まれている。これを除けば、両者は良く似ている。
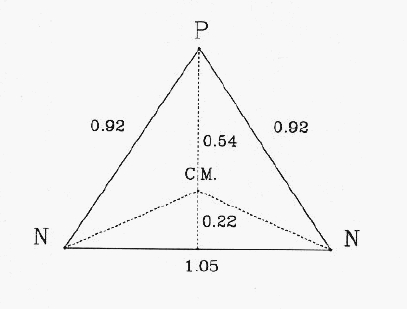
一つの簡単な設問として、「もっとも可能性の高い3核子の位置はどこだろうか?」というものがある。それは、グラフに示した通りで、その形は殆ど正三角形に近く、同一粒子である中性子同士の距離が他の2つの距離よりも少し長くなっている。それらの距離は1fm程度で、原子分子の場合と違って少し変形しても同程度の存在確率をもっている。
(グラフ)