第二章３核子束縛状態

３核子系の厳密な解を得るために、必要とは言えないが安全な方法の一つとして、ファディーフの方法がある。
L.D. Faddeev, Sov. Phys. JETP 12 (1961) 1014.

参考書：

散乱の量子論

砂川　重信　著　　岩波全書 296

The Quantum Mechanical Few-Body Problem

Walter Gloeckle 著 Springer-Verlag, Berlin Heidelberg New York Tokyo 1983

２.１ファディーフ方程式

一つの三体系には三つの二体部分系がある。先ずは二体系に働く核力だけを問題にし、その次に三核子に働く三体力を取り込んでいこう。二体力を含んだハミルトニアンから始める。

（２.１）

ここで、便宜上表記の簡単化を行う。例えば、

（２.２）

H０は三体の相対運動エネルギーで、（２.１）式を書き直せば、

（２.３）

となり、束縛状態であることから、非斉次の項は現れない。どのような現象が起っているのかを見るために、この式をこの式自体に何度か代入を繰り返してみよう。

（２.４）

これを、図にしてみれば、ある典型的な場合として、
（図）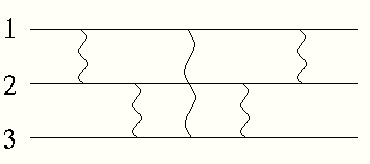

この様なものが得られる。二体の場合に既に見てきたように、グリーン関数（G０）と相互作用の部分が交互に現れている。更に、良く観察すれば、同じペア（２核子）同志の相互作用の繰り返しの場合と、異なるペアの相互作用に移る場合になっていることに気付く。さて、同じペアの部分が更にもう一度同じペアで相互作用する場合も可能である。同じペアの部分は、１度、２度、３度...と相互作用をしたものを全て取り込む必要がある。ファディーフ理論ではこれを可能する。先ず、波動関数を３つの部分に分解する。

（２.５）

（２.６）

今日ではそれぞれの部分をファディーフ要素と呼ぶ。最後の相互作用 V＿i に着目して分類したことになる。これを、元の式に代入仕直してみれば、

（２.７）

となり、これは２つの項に分けられる。第２項から、次の繰り返しをすれば分るように異なるペアの相互作用が現れる。第１項を左辺へ移項すると
（２.８）
となり、この積分核の逆（inversion）を作用させると、
（２.９）
を得る。さて、ファディーフ要素の前にある式を整理してみよう。

（２.１０）
（２.１１）
（２.１２）

よってこの式は、i-番目のペアにおける遷移行列（t - matrix ）に帰着する。即ち、これは第一章で述べた LSE 方程式を満す。

（２.１３）
従って、（２.９）式は

（２.１４）
となる。これは、３つの式が連立した方程式で、ファディーフ方程式と呼ぶ。相互作用 V ではなく、この t によって、（２.１４）式を繰り返しをしたグラフをかけば、

（図）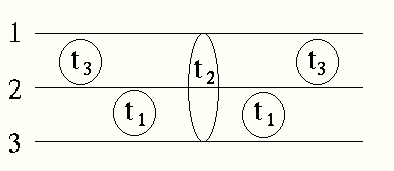

この様になる。ここで重要なことは、遷移行列 t-metrix が、次の t- matrix を繰り返す場合、必ず異なるペアを選ぶ事である。実は、この事が３体方程式が数学的に解けるかどうかに関して重要な意味をもっている。

もう少し具体的に３つの同一フェルミオンを扱うことにしよう。この場合、全体の波動関数は、全反対称状態（任意の２粒子の交換に対して、波動関数の位相を(-1)だけかえる）である。同一粒子であることから、ファディーフ要素の関数はどれも同じになり、ただ、粒子の交換によって表すことができる。それを表記すれば、粒子交換演算子 P を用いて、

（２.１５）
（２.１６）